Mathematical Preliminaries
Common Statistical Definitions
This is part of the moments math collection.Random Variables
For a space of elementary events, say , a random variable is a real number function defined on the set .
Essentially, may be considered to be a quantity which takes its values (say ) from a subset of real numbers.
We note that iff is a random variable, a function is also random.
Random variables are further quantified and classified on the basis of their distribution functions.
- Distribution Law
A rule (tabular, functional, graphical, etc) which permits one to find the probabilities of an event (a.k.a the random variable) is the distribution law for the random variable.
Distribution Functions
Every random variable is defined in terms of it’s probabilities, i.e they are characterized by the likelihood of having a particular value.
Mathematically, the cumulative distribution function of a random variable is the function whose value at every point is equal to the probability of the event :
Properties
- and
- ,
- is left continuous. (i.e., )
Types of Random Variables
On the basis of the above concepts, we now quantify random variables as:
Expectation
The expectation (expected value) of a discrete or continuous random variable is mathematically defined by:
For the continuous case, it is necessary that the integral or it’s corresponding series converges absolutely.
In generic terms, the expectation is the main characteristic defining the “position” of a random variable, i.e., the number near which its possible values are concentrated.
Similarly, due to the similarity of functions describing random variables and random variables, given a random variable related to a random variable by a functional dependence then we have:
Variance
The variance, Var{} is the measure of deviation of a random variable from the expectation as determined by:
(1)
The variance characterizes the spread in values of the random variable about its expectation.
Graphical Preliminaries
Having introduced the density function and the distribution function, it is trivial to interpret the following curves in the figure below and note, that the probability may be represented as an area between the density function and the -axis on the interval
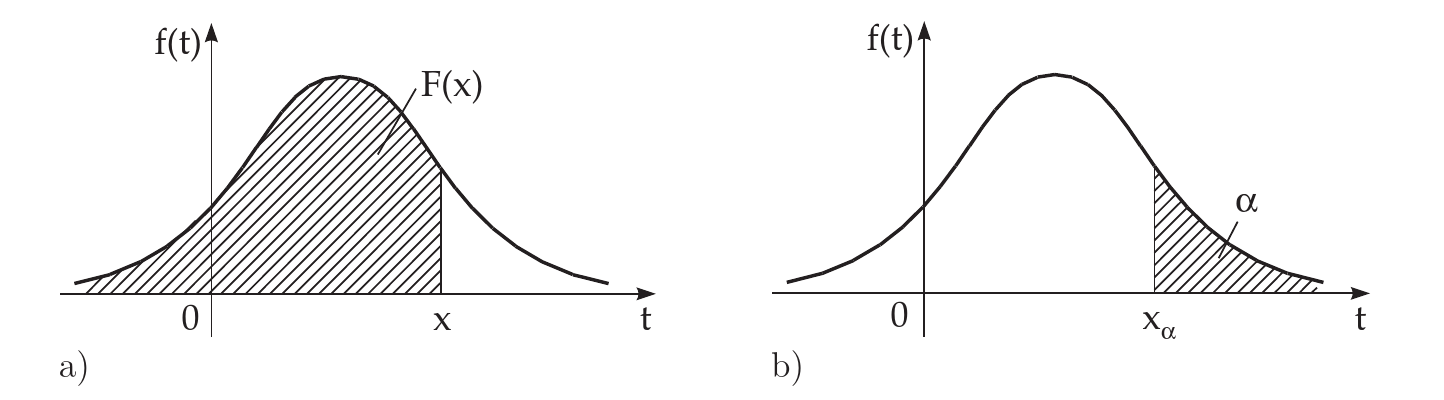
Often there is given (frequently in %) a probability value .
If holds, the corresponding value of the abscissa is called the quantile or the fractile of order
This means the area under the density function to the right of is equal to .
Remark: In the literature, the area to the left of is also used for the definition of quantile.
In mathematical statistics, for small values of , e.g., or , is also used the notion significance level of first type or type 1 error rate.
References
Bronshtein, I.N., K.A. Semendyayev, G. Musiol, and H. Mühlig. 2015. Handbook of Mathematics. Springer Berlin Heidelberg. https://books.google.co.in/books?id=5L6BBwAAQBAJ.
Bronshtein et al. (2015)↩